Quantum True Random
Number Generator

Introduction

This page aims to show some randomness tests of the quantum card "IDQ Quantis". We use software 'dieharder' and the GCD test. True Random Numbers can be generated using this card in the SINAPAD portal HERE.

Dieharder Test

This section shows the output of the dieharder test. We output 10,000,000 samples of unsigned 32-bit integers.

#=============================================================================#
#            dieharder version 3.31.1 Copyright 2003 Robert G. Brown          #
#=============================================================================#
   rng_name    |           filename             |rands/second|
     file_input|                           q.rnd|  3.95e+06  |
#=============================================================================#
        test_name   |ntup| tsamples |psamples|  p-value |Assessment
#=============================================================================#
# The file file_input was rewound 1 times
   diehard_birthdays|   0|       100|     100|0.14890535|  PASSED  
# The file file_input was rewound 11 times
      diehard_operm5|   0|   1000000|     100|0.00005311|   WEAK   
# The file file_input was rewound 24 times
  diehard_rank_32x32|   0|     40000|     100|0.14222990|  PASSED  
# The file file_input was rewound 30 times
    diehard_rank_6x8|   0|    100000|     100|0.43266760|  PASSED  
# The file file_input was rewound 32 times
   diehard_bitstream|   0|   2097152|     100|0.24543060|  PASSED  
# The file file_input was rewound 53 times
        diehard_opso|   0|   2097152|     100|0.00000012|  FAILED  
# The file file_input was rewound 67 times
        diehard_oqso|   0|   2097152|     100|0.33273879|  PASSED  
# The file file_input was rewound 74 times
         diehard_dna|   0|   2097152|     100|0.23963512|  PASSED  
# The file file_input was rewound 74 times
diehard_count_1s_str|   0|    256000|     100|0.43746621|  PASSED  
# The file file_input was rewound 87 times
diehard_count_1s_byt|   0|    256000|     100|0.00533304|  PASSED  
# The file file_input was rewound 87 times
 diehard_parking_lot|   0|     12000|     100|0.33862926|  PASSED  
# The file file_input was rewound 88 times
    diehard_2dsphere|   2|      8000|     100|0.99040035|  PASSED  
# The file file_input was rewound 88 times
    diehard_3dsphere|   3|      4000|     100|0.99736995|   WEAK   
# The file file_input was rewound 111 times
     diehard_squeeze|   0|    100000|     100|0.00008099|   WEAK   
# The file file_input was rewound 111 times
        diehard_sums|   0|       100|     100|0.12278142|  PASSED  
# The file file_input was rewound 112 times
        diehard_runs|   0|    100000|     100|0.85911788|  PASSED  
        diehard_runs|   0|    100000|     100|0.44121218|  PASSED  
# The file file_input was rewound 125 times
       diehard_craps|   0|    200000|     100|0.00000352|   WEAK   
       diehard_craps|   0|    200000|     100|0.06085085|  PASSED

The dieharder software has marked PASSED in 14 of 19 tests, WEAK in 4 tests, and FAILED in 1 test.

The GCD Randomness Test

This test is explained in G. Marsaglia and W. W. Tsang's paper Some difficult-to-pass tests of randomness. The goal is to generate random pairs u,v and compute their GCD. The result of this procedure generates three lists.
(1) The number of iterations needed to compute the GCD (using the Euclidean algorithm) is independent and indentically distributed (iid).
(2) The sequence of partial quotients is not iid.
(3) The list of GCDs is iid.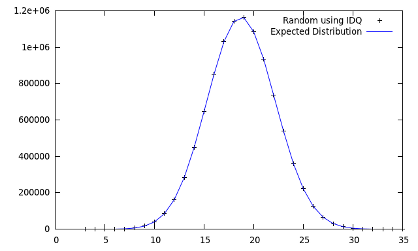

Fig 1 - Distribution of the number of iterations computing the GCD.

Fig. 1 shows that the experimental distribution is very closed to the expected distribution.

Quantum True Random Number Generator

Introduction

Dieharder Test

The GCD Randomness Test

Quantum True Random
Number Generator